Reinforcement learning versus bandit

Reinforcement Learning versus Bandit

Recently, I fulfill my PhD Qulifying Exam which focuses on Bandit and its application on online recommender system (RecSys). My supervisor keeps challenging the motivation of modeling RecSys as bandit problem compared to other Reinforcement Learning formulations. Caused quite few detail explanations are found online, I would like to share my understanding of what differs bandit from other RL formulation in this post.

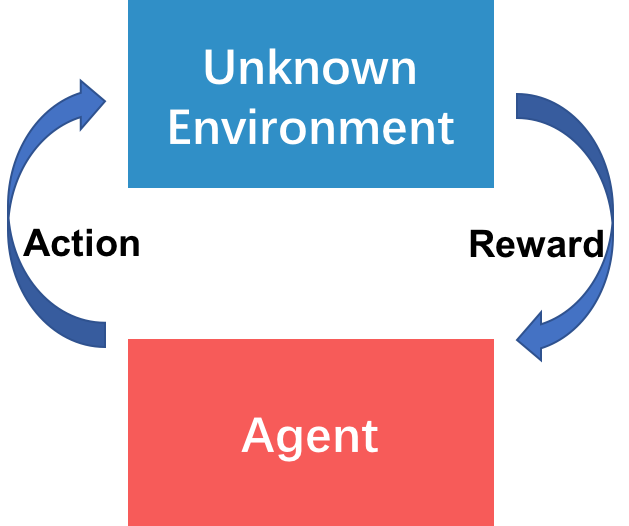
The exploitation-exploration tradeoff is emphasized when tackling canonical problem of sequential decision making under uncertainty. More concretely, an agent sequentially interacts with unkown environment and receive the rewards as shown in Fig. 1. The ultimate objective is to maximize the cumulative reward. For one thing, the agent exploits known optimal action. For another, the agent explores unkown environment. Exploitation-exploration tradeoff is always formalized as Reinforcement Learning including Multi-Armed Bandit (MAB), Markov Decision Process (MDP), or Partially observable Markov Decision Process (POMDP). Our question is for what applications bandit forumation is more suitable.

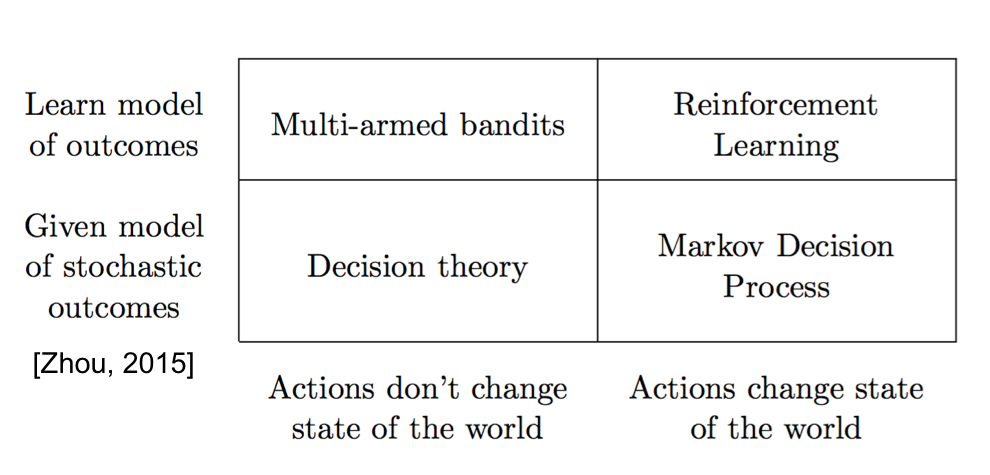
According to many tutorials of Reinforcement Learning, the unknown environment can be described by multiple elements including observations $\Omega$, states $S$, actions $A$, reward function $R$, state transition probability $T$, and conditional observation probabilities $O$. Bandit, MDP, and POMDP models the environment by considering different elements respectively as shown in Fig. 2. More concretely, Bandit only explores which actions are more optimal regardless of state. Actually, the classical multi-armed bandit policies assume the i.i.d. reward for each action (arm) in all time. [1] also names bandit as one-state or stateless reinforcement learning and discuss the relationship among bandit, MDP, RL, and decision theory as shown in Fig. 3.

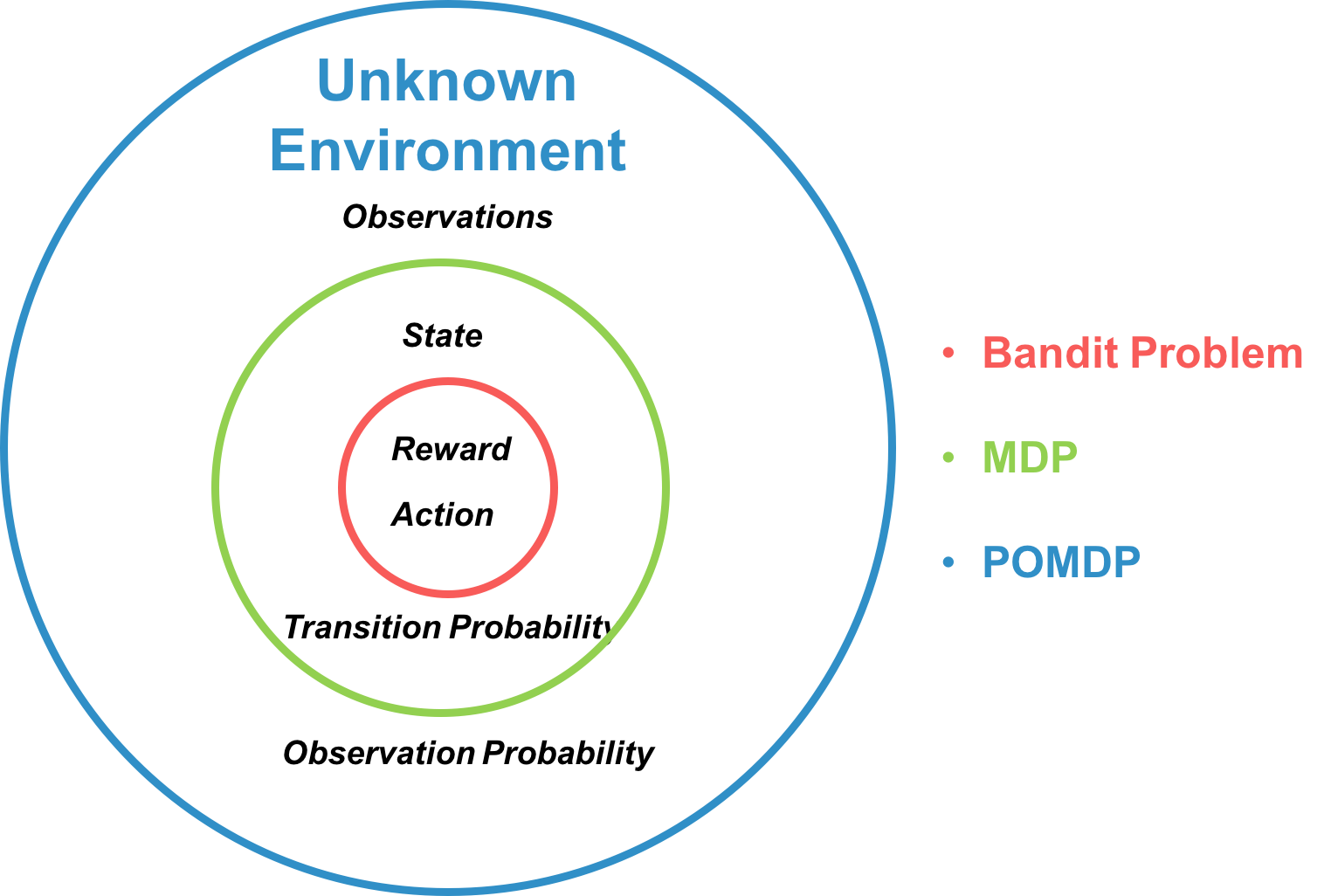
Compared to one-state RL, i.e. multi-armed bandit. MDP explores not only the stochastic reward function but also the state and state transition probability. POMDP further generalizes MDP by assuming the hidden state and exploring the observations and observation state probability. We use the restaurant selection problem as example. We may often go to our favorite restaurant and try some new sometimes to find a potential better one. If our preference for every restaurant never changes, the bandit is very suitable formulation. If our preference changes to Chinese food after having Japanese food, then modeling and exploring the state transition is more suitable. Finally, if the preference of restaurant are decided by many hidden factors, e.g. hidden interest, mood, and etc, it is more preferable to consider POMDP.

Multi-armed bandit is widely applied to online recommendation to make personlized article recommenation [Li, Lihong]. Intuitively, user interests change very quickly. For instance, one user are highly unlikely to buy a Playstation 4 if have already bought one. As a result, it seems that modeling recommendation as MDP or POMDP is more suitable than bandit problem.

However, in my opinion, MDP and bandit focus on exploring different elements and do not conflict. We take Q-Learning as example as shown in Fig. 4. I suppose that line 7 explores the state transition. If we always select the action with maximum expected reward in each time step, Q-learning is equivalent to pure exploitation. Pure exploitation can stuck in suboptimal actions for stochastic rewards. For instance, in state $s_1$ with two actions, a randomly generated large reward may mislead the policy and stuck in suboptimal action. As a result, in Line 5, Q-Learning select the actions using $\epsilon-greedy$ which is most basic bandit policy.

For online recommender system, in my opinion, (PO)MDP focuses on exploring user interests change and bandit focuses on exploring stochastic reward. (PO)MDP and bandit combined should lead to a better result.

1. Zhou, Li. “A survey on contextual multi-armed bandits.” CoRR, abs/1508.03326 (2015).
2. Li, Lihong, et al. “A contextual-bandit approach to personalized news article recommendation.” Proceedings of the 19th international conference on World wide web. ACM, 2010.